Question

Angle

C

CC is inscribed in circle

O

OO.

A

B

‾

AB

start overline, A, B, end overline is a diameter of circle

O

OO.

What is the radius of circle

O

OO?

Answer 1

90 degrees

Explanation:

Answer 2

An inscribed angle is defined as the half of its intercepted arc. It's important to notice that the subtended arc by angle C is 180°, because it's have of the total arc length.

`C=(1)/(2) (180\°)=90\°`

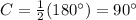
Therefore, angle C is a right angle.

Now, in the image attached you can notice that triangle ABC has one acute angle of 46° and one right angle. We already know that the sum of all three internal angles of a triangle must be equal to 180°.

`90\° + 46\° + B=180\°\\B=180\° - 46\° - 90\° = 44\°`

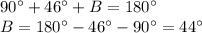
On the other hand, notice that the diameter of the circle represents the hypothenuse for the right triangle. To find the hypothenuse, we need to know the length of one leg at least.

Therefore, there's no enough information to find the hypothenuse, which implies we can't find the diameter/radius.