Question

Last month maria purchased a new cell phone for $500. the store manager told her that her cell phone would depreciate by 70% every 6 months. maria thinks she will want to replace her phone after a while. what will be the value (V) of her phone if she tries to trade it in after 2 years? select ALL that apply.

A: V=500(0.70)⁴
B: V=500(0.30)⁴
C: V=500(0.30)²
D: V=500(1 - 0.70)⁴
E: V=0.70(500)⁴
F: V=0.30(500)²​

Answer 1

We have been given that last month Maria purchased a new cell phone for $500. The store manager told her that her cell phone would depreciate by 70% every 6 months.

We know that an exponential function is in form
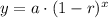`y=a\cdot (1-r)^x`, where,

y = Final value,

a = Initial value,

r = Decay rate in decimal form,

x = Time in years.

Let us convert
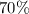`70\%` into decimal form.

`70\%=(70)/(100)=0.70`

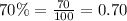
Initial value of car is 500, so
`a=500`.

Since value of phone depreciates every months, so value of phone will depreciate twice in a year.

Upon substituting our given values in exponential decay function, we will get:

`V=500(1-0.70)^(2x)`

To find the value of phone after 2 years, we will substitute
`x=2` in our equation.

`V=500(1-0.70)^(2(\cdot 2))`

`V=500(1-0.70)^(4)`

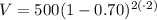
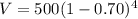
Therefore, option D is the correct choice.

Let us simplify our equation.

`V=500(0.30)^(4)`

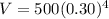
Therefore, option B is correct as well.