Question

To catch a frisbee, a dog leaps into air with an initial velocity of 14 feet per second. Write a model for the height of the dog above the ground. After how many seconds does the dog land on the ground?

Answer 1

Model:
`y = 14t+(1)/(2)(32.16)t^(2)`

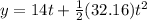
The dog land on the ground after 0.8706 seconds.

Explanation:

The model that said the height of the dog above the ground is a model of uniform acceleration motion, so it is:

`y = y_0+v_0t+(1)/(2)gt^(2)`

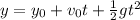
Where
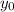`y_0` is the initial height,
`v_0` is the initial velocity and
`g` is the gravity.

So, replacing
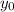`y_0` by zero,
`v_0` by 14 feet per second and
`g` by
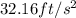`32.16 ft/s^2`, we get that the model for the height of the dog above the ground is:

`y = 14t+(1)/(2)(32.16)t^(2)`

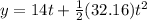
Then, the time t when the dog land on the ground is calculated replacing
`y` by zero and solving for t as:

`y = 14t+(1)/(2)(32.16)t^(2)\\0 = 14t+(1)/(2)(32.16)t^(2)\\0 =t (14 - 16.08t)`

Now, we have two possible solutions:

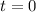`t=0` or
`14-16.08t=0`

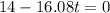
Taking into account that t=0 is the time when the dog leaps into air, the time when the dog land on the ground is equal to 0.8706 seconds and it is calculated as:

`14-16.08t=0\\14=16.08t\\(14)/(16.08)=t\\t=0.8706`