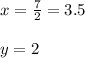Question

Решить систему методом сложения:{4x-6y=2
2x-y=5

Answer 1

`x=(7)/(2) =3.5\\\\y=2`

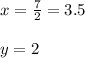
Explanation:

The addition method (elimination method) allows us to combine two equations in such a way that the resulting equation has only one variable. Then we can use simple algebraic methods to solve that variable

Let:

`4x-6y=2\hspace{10}(1)\\\\and\\\\2x-y=5\hspace{15}(2)`

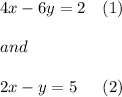
Let's multiply (2) by -2:

`-2*(2):\\\\2x(-2)-y(-2)=5(-2)\\\\-4x+2y=-10\hspace{12}(-2*(2))`

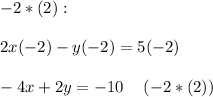
Now, add (1) and (-2*(2)):

`(1)+(-2*(2)):\\\\4x+(-4x)-6y+(2y)=2+(-10)\\\\-4y=-8`

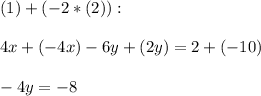
Hence, solving for y:

`y=(-8)/(-4) =2`

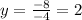
Replacing y into (2):

`2x-(2)=5`

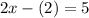
Solving for x:

`2x=5+2\\\\2x=7\\\\x=(7)/(2) =3.5`

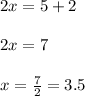
Therefore:

`x=(7)/(2) =3.5\\\\y=2`