Answer:
Domain = R
Range = (-∞, 4)
Hor. asymp = y=4
Y intercept: f(0) = (0,2)
end behaviour:
x → -∞: f(x) → 4
x→ ∞: f(x) → -∞
Explanation:
For the domain, it is R because e^x works for all values of x
For the range, y will never be above 4.
The hor. asymptote is found via
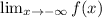 there the e term will be zero, so what is left is y=4.
there the e term will be zero, so what is left is y=4.
Y intercept, fill in f(0)
end behaviour: for small x, y goes to the asymptote, for large x, y goes to minus infinity.