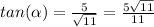Question

If sin = O =5/6, what are the values of cos O and tan O? (2 points)​

Answer 1

As trigonometry property:

(sinO)^2 + (cosO)^2 = 1

tanO = sinO/cosO

Then, if sinO = 5/6 = 0.83

=> (5/6)^2 + (cosO)^2 = 1

=> cosO = +/- sqrt(1 - (5/6)^2) = +/- 0.55

=>tanO = +/- 0.83/0.55 = +/- 1.51

Hope this helps!

:)

Answer 2

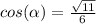`cos(\alpha )=(√(11) )/(6)` and
`tan(\alpha )=(5√(11) )/(11)`

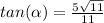
Explanation:

First we would need to solve for the missing leg in order to figure out the remaining answers.

To do this we can use the Pythagorean Theorem a² + b² = c²

Our missing leg in this case is a, so solving for a gives us
`a=\sqrt{c^(2) -b^(2) }`

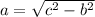
Here our b is 5 and our c is 6. So plugging in these values we get
`a=\sqrt{(6)^(2)-(5)^(2) } =√(36-25) =√(11)`

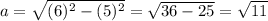
With this missing leg being solved, we can use trig identities to solve for cos and tan

I used the trig identity
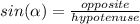`sin(\alpha )=(opposite)/(hypotenuse)` to set up the triangle in the attached image. We can use the trig identity
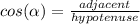`cos(\alpha)=(adjacent)/(hypotenuse)` which would give us
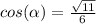`cos(\alpha )=(√(11) )/(6)` and we can use the trig identity
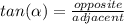`tan(\alpha ) = (opposite)/(adjacent)` which would give us
`tan(\alpha )=(5)/(√(11) ) =(5√(11) )/(11)`