Answer: 3597 kJ of heat
Step-by-step explanation:
According to ideal gas equation:
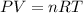
P = pressure of gas = 5.00 atm
V = Volume of gas = 8.00 L
n = number of moles = ?
R = gas constant =
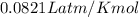
T =temperature =
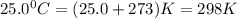

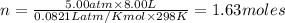
As it is given :
1 mole of propane produces = 2220 kJ of heat
Thus 1.63 moles of propane produces =
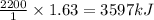
Thus 3597 kJ of heat is produced