Answer:
Discriminant = 84
The polynomial has two real distinct roots
Explanation:
Given:
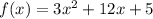
To find: discriminant of the given function and number of distinct real zeros
Solution:
For a polynomial
 , discriminant is given by
, discriminant is given by
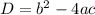
If
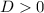 , then the polynomial has two real and distinct roots.
, then the polynomial has two real and distinct roots.
If
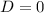 then the polynomial has two real and equal roots.
then the polynomial has two real and equal roots.
If D<0 then roots are not real.
Here, in
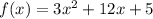
a = 3, b = 12 and c = 5
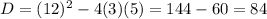
As D > 0, the polynomial has two real distinct roots.