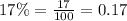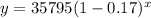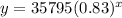We have been given that a new car, originally worth $35,795, depreciates at a rate of 17% per year. The value of the car can be represented by the equation
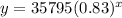 , where x represents the number of years since purchase and y represents the value (in dollars) of the car.
, where x represents the number of years since purchase and y represents the value (in dollars) of the car.
To find the value of car of after 5 years, we will substitute
 in our given equation as:
in our given equation as:
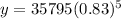

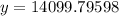
Upon rounding to nearest tenth, we will get:
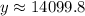
Therefore, the car will be worth $14,099.8 after 5 years it is first purchased.
Since $14,099.8 is less than original value of car, therefore, we know hat value of car is depreciating and $14,099.8 is correct answer.
We also know that an exponential decay function is in form
 , where,
, where,
y = Final value after t years,
a = Initial value,
r = Decay rate in decimal form,
x= Time.