Question

5x^2-25x=125 solve by completeing the square

Answer 1

x = 10, -15

Explanation:

We can start right away by dividing both sides of our equation by 5 to get the reduced form
`x^2-5x=25`.

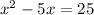To "complete the square," or turn the left side of the equation into something we can factor into a perfect square, it helps to remember that for any binomial x - a:

`(x-a)^2=x^2-2ax+a^2`

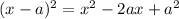
To "complete" our square, we'll need to add an a² to either side of the equation. To find a, we can set 5x = 2ax and solve:

`5x=2ax\\5/2=a\\25/4=a^2`

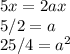
Let's add that a² to both sides and simplify!

`x^2-5x+(25)/(4)=25+(25)/(4)\\\\(x-(5)/(2))^2=(125)/(4)\\\\x-(5)/(2)=\pm\sqrt{(125)/(4) } \\\\x=\pm(25)/(2)-(5)/(2)`

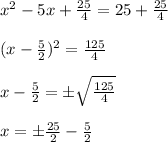
Now we're ready to solve for both value of x:

`x=(25)/(2)-(5)/(2)=(20)/(2) =10\\\\x=-(25)/(2)- (5)/(2)=-(30)/(2) =-15`

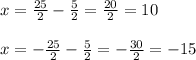
So our solutions are x = 10 and x = -15

Answer 2

x=5+5√5/2

Explanation: