Question

g Given an array, the task is to design an efficient algorithm to tell whether the array has a majority element, and, if so, to find that element. The elements of the array are not necessarily from some ordered domain like the integers, and so there can be no comparisons of the form "is A[i] ≥ A[j]?". (Think of the array elements as GIF files, say.) However you can answer questions of the form: "is A[i] = A[j]?" in constant time

Answer 1

If there is a majority element in the array it will be the median. Thus,

just run the linear time median finding algorithm, and compare the result with all the elements of the array (also linear time). If
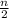`(n)/(2)`elements are the same as the median, the median is a ma majority element. If not, there is none.

Suppose now that the elements of the array are not from some ordered domain like the integers, and so there can be no comparisons of the form "is the ith element of the array greater than the jth element of the array?" However you can answer questions of the form:

"Are the ith and jth elements of the array the same?" in constant time. Such

queries constitute the only way whereby you can access the array. (Think of the elements of the array as GIF files, say.) Notice that your solution above cannot be used now.