Answer:
Step-by-step explanation:
The ball was moving with velocity of 20 m /s earlier in horizontal direction . Due to kicking, additional V velocity was added to it at 40° because he kicked it at this angle but the ball travelled in the direction of resultant which was making an angle of 30° with the horizontal .
From the relation of inclination of resultant
Tan θ = V sinα / (u + V cosα) where α is angle between u and V , θ is inclination of resultant
Tan30 =
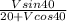

20 + .766 V = 1.11 V
20 = .344 V
V = 58 m /s
To know the force , we shall apply concept of impulse
F x t = mv , F is force for time t creating a change of momentum mv
F x .1 = .4 x 58
F = 232 N