Answer:
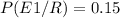
Explanation:
Hola!
La comañía en cuestión usa 4 empresas de transporte para realizar envios. Llamemos "E" al evento de que la empresa haya sido seleccionada para un envío:
E1: La empresa A1 realiza el envío ⇒ P(E1)= 0.15
E2: La empresa A2 realiza en envío ⇒ P(E2)= 0.30
E3: La empresa A3 realiza el envío ⇒ P(E3)= 0.35
E4: La empresa A4 realiza el envío ⇒ P(E4)= 0.20
Y también conoces las probabilidades de que un envío llegue con retraso, sabiendo cual es la empresa que realizó el envío. Llamemos "R" al evento que el envío llegó con retraso. Las probabilidades mencionadas son condicionales y se simbolizan de la siguiente manera:
P(R/E1)= 0.07
P(R/E2)= 0.08
P(R/E3)= 0.05
P(R/E4)= 0.09
Tienes que calcular la probabilidad de que un embarque que ha sido entregado con retraso, haya sido enviado por la empresa A1.
Esta probabilidad también es condicional, queremos saber la probabilidad de E1 sabiendo que ya ha pasado R, se simboliza de la siguiente manera:
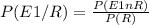
Para poder calcularla necesitas averiguar el valor de la probabilidad de intersección entre E1 y R, P(E1∩R), y el valor de la probabilidad de R, P(R).
La probabilidad de R es una probabilidad marginal y es igual a:
P(R)= P(E1∩R)+P(E2∩R)+P(E3∩R)+P(E4∩R)
Para calcular los valores de las intersecciones debes aplicar la definición de probabilidad condicional:
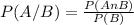entonces P(A∩B)= P(A/B)*P(B)
Entonces:
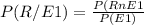⇒ P(E1∩R)= P(R/E1)*P(E1)= 0.07*0.15= 0.0105
P(E2∩R)= P(R/E2)*P(E2)= 0.08*0.30= 0.024
P(E3∩R)= P(R/E3)*P(E3)=0.05*0.35= 0.0175
P(E4∩R)= P(R/E4)*P(E4)= 0.09*0.20= 0.018
Ahora puedes calcular la probabilidad de que el envío llegue con retraso:
P(R)= 0.0105+0.024+0.0175+0.018= 0.07
Por último queda calcular la probabilidad solicitada:
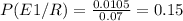
Espero que tengas un buen día!