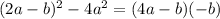Question

4. Factor (2a – b)^2- 4a^2

Answer 1

(4a - b)(-b)

Explanation:

If we let x = 2a - b and y = 2a, our expression now looks like

`x^2-y^2`

This kind of a expression is a common pattern in algebra called a difference of squares, and it can be factored like this (for a visual proof, see the attached image, courtesy of Great Maths Teaching Ideas):

`x^2-y^2=(x+y)(x-y)`

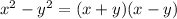
Replacing x and y with 2a -b and 2a, our expression now becomes

`[(2a-b)+2a][(2a-b)-2a]\\=(2a-b+2a)(2a-b-2a)\\=(4a-b)(-b)`

So in factored form,

`(2a-b)^2-4a^2=(4a-b)(-b)`

Answer 2

(-b) (4a-b)

Explanation:

(2a – b)^2- 4a^2

Let m = 2a-b

m^2 - (2a)^2

We know this is the difference of squares

x^2 - y^2 = (x-y)(x+y)

(m-2a) (m+2a)

Replace m with 2a -b

(2a -b-2a) (2a-b+2a)

Simplify

(-b) (4a-b)