Question

The president of a university claimed that the entering class this year appeared to be larger than the entering class from previous years but their mean SAT score is lower than previous years. He took a sample of 20 of this year's entering students and found that their mean SAT score is 1,501 with a standard deviation of 53. The university's record indicates that the mean SAT score for entering students from previous years is 1,520. He wants to find out if his claim is supported by the evidence at a 5% level of significance. Referring to Scenario 9-9, what is the critical value

Answer 1

Critical value = -1.729

Step by Step explanation:

Given:

n = 20

X' = 1501

Standard deviation = 53

Mean, u = 1520

Level of significance, a = 0.05

The null and alternative hypotheses:

H0 : u = 1520

H1 : u < 1520

This is a lower tailed test.

Degrees of freedom, df = 20 - 1 = 19

For critical value:

`t critical = - t_a, _d_f`

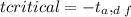
From t table df = 19, one tailed

`t critical = -t _0._0_5, _1_9 = -1.729`

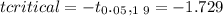
Critical value = -1.729

Decision: Reject null hypothesis H0, if test statistic Z, is less than critical value.

Test statistic Z =

`Z = (X' - u)/(\sigma / √(n))`

`Z = (1501 - 1520)/(53/ √(20))= -1.603`

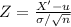
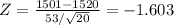
Z = -1.603

For p-value:

From excel,

P(t< -1.603) = t.dist( -1.603, 19, 1)

= 0.06269

≈ 0.0627

P value = 0.0627

Since test statistic Z, -1.603, is greater than critical value, -1.729, we fail to reject the null hypothesis H0.

There is not enough statistical evidence to conclude that mean is less than 1520.

Answer 2

Explanation:

To test the hypothesis is the mean SAT score is less than 1520 at 5% significance level

The nul hypothesis is

`H_0; \mu \geq 1520`

The alternative hypothesis is

`H_0 ; \mu\leq 1520`

The test statistic is

`t=(\bar x- \mu)/(((s)/(√(n) ) ))`

`t= (1501-1520)/(((53)/(√(20) ) )) \\\\=-1.603`

The t - test statistics is -1.603

The t - critical value is,

The small size is small and left tail test.

Look in the column headed
`\alpha = 0.05` and the row headed in the t - distribution table by using degree of freedom is,

d.f = n - 1

= 20 - 1

= 19

The t - critical value is -1.729

The conclusion is that the t value corresponds to sample statistics is not fall in the critical region, so the null hypothesis is not rejected at 5% level of significance.

there is insignificance evidence ti indicate that the mean SAT score is less than 1520. The result is not statistically significant