Answer:
Critical value = -1.729
Step by Step explanation:
Given:
n = 20
X' = 1501
Standard deviation = 53
Mean, u = 1520
Level of significance, a = 0.05
The null and alternative hypotheses:
H0 : u = 1520
H1 : u < 1520
This is a lower tailed test.
Degrees of freedom, df = 20 - 1 = 19
For critical value:
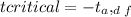
From t table df = 19, one tailed
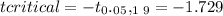
Critical value = -1.729
Decision: Reject null hypothesis H0, if test statistic Z, is less than critical value.
Test statistic Z =
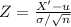
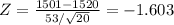
Z = -1.603
For p-value:
From excel,
P(t< -1.603) = t.dist( -1.603, 19, 1)
= 0.06269
≈ 0.0627
P value = 0.0627
Since test statistic Z, -1.603, is greater than critical value, -1.729, we fail to reject the null hypothesis H0.
There is not enough statistical evidence to conclude that mean is less than 1520.