Answer:
![\omega=0.37 [rad/s]](https://img.qammunity.org/2021/formulas/physics/college/dx9b13wjgr03jzr466ndghxy4bh4amd3lq.png)
Step-by-step explanation:
We can use the conservation of the angular momentum.
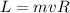
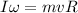
Now the Inertia is I(professor_stool) plus mR², that is the momentum inertia of a hoop about central axis.
So we will have:
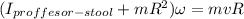
Now, we just need to solve it for ω.
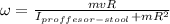

![\omega=0.37 [rad/s]](https://img.qammunity.org/2021/formulas/physics/college/dx9b13wjgr03jzr466ndghxy4bh4amd3lq.png)
I hope it helps you!