Question

Evaluate the expression 5^x- 3^x5 x −3 x 5, start superscript, x, end superscript, minus, 3, start superscript, x, end superscript for x=2x=2x, equals, 2.

Answer 1

5^x - 3^x for x=2 is 16

Explanation:

Answer 2

Question:

Evaluate the expression 5^x - 3^x for x=2

Answer:

5^x - 3^x for x=2 is 16

Explanation:

Given

5^x - 3^x

x=2

Required

Evaluate

When fazed with question like this all you need is to substitute the value of x (or any other variable{s} used) in the expression.

Recall that x = 2

So, you have to substitute 2 for x in 5^x - 3^x

This gives

`5^2 - 3^2`

This can be further solved in 2 ways

1. Solve directly

`5^2 - 3^2`

=
`25 - 9`

= 16

2. Expand using difference of two squares.

Difference of two squares is represented by

`a^2 - b^2 = (a + b) (a - b)`

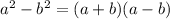
By comparison

`5^2 - 3^2` becomes

`5^2 - 3^2 = (5 + 3) (5 - 3)`

`5^2 - 3^2 = (8) (2)`

`5^2 - 3^2 = 8 * 2`

`5^2 - 3^2 = 16`

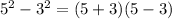
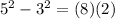
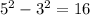
For both ways, we'll arrive at the same answer.

Hence, 5^x - 3^x for x=2 is 16