Question

4. A small high school holds its graduation ceremony in the gym. Because of seating constraints, students are limited to a maximum of four tickets to graduation for family and friends. The vice principal knows that historically 30% of students want four tickets, 25% want three, 25% want two, 15% want one, and 5% want none. (a) Let X ¼ the number of tickets requested by a randomly selected graduating student, and assume the historical distribution applies to this rv. Find the mean and standard deviation of X. (b) Let T ¼ the total number of tickets requested by the 150 students graduating this year. Assuming all 150 students’ requests are independent, determine the mean and standard deviation of T. (c) The gym can seat a maximum of 500 guests. Calculate the (approximate) probability that all students’ requests can be accommodated. [Hint: Express this probability in terms of T. What distribution does T have?]

Answer 1

(a) The mean and standard deviation of X is 2.6 and 1.2 respectively.

(b) The mean and standard deviation of T are 390 and 180 respectively.

(c) The distribution of T is N (390, 180²). The probability that all students’ requests can be accommodated is 0.7291.

Explanation:

(a)

The random variable X is defined as the number of tickets requested by a randomly selected graduating student.

The probability distribution of the number of tickets wanted by the students for the graduation ceremony is as follows:

X P (X)

0 0.05

1 0.15

2 0.25

3 0.25

4 0.30

The formula to compute the mean is:

`\mu=\sum x\cdot P(X)`

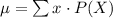
Compute the mean number of tickets requested by a student as follows:

`\mu=\sum x\cdot P(X)\\=(0* 0.05)+(1* 0.15)+(2* 0.25)+(3* 0.25)+(4* 0.30)\\=2.6`

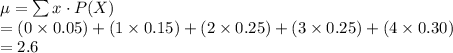
The formula of standard deviation of the number of tickets requested by a student as follows:

`\sigma=\sqrt{E(X^(2))-\mu^(2)}`

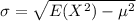
Compute the standard deviation as follows:

`\sigma=\sqrt{E(X^(2))-\mu^(2)}\\=\sqrt{[(0^(2)* 0.05)+(1^(2)* 0.15)+(2^(2)* 0.25)+(3^(2)* 0.25)+(4^(2)* 0.30)]-(2.6)^(2)}\\=√(1.44)\\=1.2`

Thus, the mean and standard deviation of X is 2.6 and 1.2 respectively.

(b)

The random variable T is defined as the total number of tickets requested by the 150 students graduating this year.

That is, T = 150 X

Compute the mean of T as follows:

`\mu=E(T)\\=E(150\cdot X)\\=150* E(X)\\=150* 2.6\\=390`

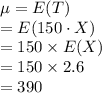
Compute the standard deviation of T as follows:

`\sigma=SD(T)\\=SD(150\cdot X)\\=√(V(150\cdot X))\\=\sqrt{150^(2)}* SD(X)\\=150* 1.2\\=180`

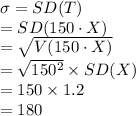
Thus, the mean and standard deviation of T are 390 and 180 respectively.

(c)

The maximum number of seats at the gym is, 500.

According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sum of values of X, i.e ∑X, will be approximately normally distributed.

Here T = total number of seats requested.

Then, the mean of the distribution of the sum of values of X is given by,

`\mu_(T)=n* \mu_(X)=390`

And the standard deviation of the distribution of the sum of values of X is given by,

`\sigma_(T)=n* \sigma_(X)=180`

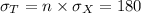
So, the distribution of T is N (390, 180²).

Compute the probability that all students’ requests can be accommodated, i.e. less than 500 seats were requested as follows:

`P(T<500)=P((T-\mu_(T))/(\sigma_(T))<(500-390)/(180))\\=P(Z<0.61)\\=0.72907\\\approx 0.7291`

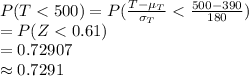
Thus, the probability that all students’ requests can be accommodated is 0.7291.