Question

An article in the Archives of Internal Medicine reported that in a sample of 244 men, 73 had elevated total cholesterol levels (more than 200 milligrams per deciliter). In a sample of 232 women, 44 had elevated cholesterol levels.Can you conclude that the proportion of men with elevated cholesterol levels is greater than the proportion of women? Let M denote the proportion of men with elevated cholesterol levels and let W denote the proportion of women with elevated cholesterol levels. Use the level of significance and the critical value method. (a) Write the hypotheses for the test.(b) Calculate the difference in sample proportions between groups.(c) Using 2PropZTest, calculate a P-value.(d) Fill in the blanks to explain what the P-value means: If there is ____________ between the proportions of high cholesterol, then there is a ___ % chance that there is a _______ or _______ percentage point difference between the high cholesterol rates.(e) What is your decision about the null hypothesis? Why?

Answer 1

We conclude that the null hypothesis is rejected which means the proportion of men with elevated cholesterol levels is greater than the proportion of women.

Explanation:

We are given that an article in the Archives of Internal Medicine reported that in a sample of 244 men, 73 had elevated total cholesterol levels.

In a sample of 232 women, 44 had elevated cholesterol levels.

Let
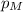`p_M` = population proportion of men with elevated cholesterol levels.

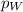`p_W` = population proportion of women with elevated cholesterol levels.

(a) Null Hypothesis,
`H_0` :
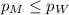`p_M \leq p_W` {means that the proportion of men with elevated cholesterol levels is smaller than or equal to the proportion of women}

Alternate Hypothesis,
`H_A` :
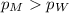`p_M > p_W` {means that the proportion of men with elevated cholesterol levels is greater than the proportion of women}

The test statistics that would be used here Two-sample z test for proportions;

T.S. =
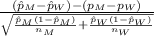`\frac{(\hat p_M-\hat p_W)-(p_M-p_W)}{\sqrt{(\hat p_M(1-\hat p_M))/(n_M) +(\hat p_W(1-\hat p_W))/(n_W)} }` ~ N(0,1)

where,
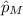`\hat p_M` = sample proportion of men with elevated cholesterol levels =
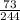`(73)/(244)` = 0.299

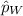`\hat p_W` = sample proportion of women with elevated cholesterol levels =
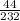`(44)/(232)` = 0.189

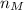`n_M` = sample of men = 244

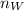`n_W` = sample of women = 232

(b) The difference in sample proportions between groups is given by =
`\hat p_M-\hat p_W` = 0.299 - 0.189 = 0.11

(c) So, the test statistics =
`\frac{(0.299-0.189)-(0)}{\sqrt{(0.299(1-0.299))/(244) +(0.189(1-0.189))/(232)} }`

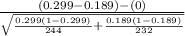
= 2.82

The value of z test statistics is 2.82.

Now, the P-value of the test statistics is given by;

P-value = P(Z > 2.82) = 1 - P(Z < 2.82)

= 1 - 0.9976 = 0.0024

(d) If there is difference between the proportions of high cholesterol, then there is a 95% chance that there is a 11% percentage point difference between the high cholesterol rates.

(e) Since, in the question we are not given with the level of significance so we assume it to be 5%.

As the P-value of the test statistics is less than the level of significance as 0.0024 < 0.05, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the proportion of men with elevated cholesterol levels is greater than the proportion of women.