Answer:
The volume of the hemisphere = 496741.6 m³
Explanation:
Volume of a sphere is= (4/3) × π × r³
r is the radius
π is 22/7
hemisphere is half of an sphere,
so the volume of henisphere is (2/3) × π × r³
Given that ;
r = 61.9 m
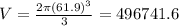
therefore, the volume of the hemisphere is 496741.6 m³