Answer:
t = 5.94x10⁹ years.
Step-by-step explanation:
The time of the explosion can be calculated using the decay equation:
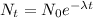
Where:
N(t): is the quantity of the element at the present time
N(0): is the quantity of the element at the time of explosion
λ: is the decay constant
t: is the time
Knowing that the present U-235/U-238 ratio is 0.00700 and that at the time of the explosion there were equal amount of U-235 and U-238, we have:
 (1)
(1)
The decay constant is equal to:
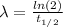
For the U-235 we have:
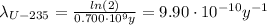
For the U-238 we have:
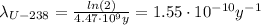
By introducing the values of
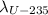 and
and
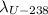 into equation (1) we have:
into equation (1) we have:

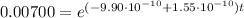
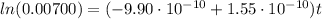
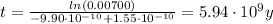
Therefore, the star exploded 5.94x10⁹ years ago.
I hope it helps you!