Answer:
1)
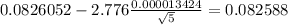

b)
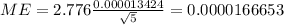
And we want 2/3 of the margin of error so then would be:
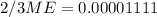
The margin of error is given by this formula:
 (1)
(1)
And on this case we have that ME =0.00001111016 and we are interested in order to find the value of n, if we solve n from equation (1) we got:
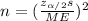 (2)
(2)
Replacing we got:
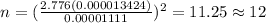
So the answer for this case would be n=12 rounded up to the nearest integer
Explanation:
Information given
0.082601, 0.082621, 0.082589, 0.082617, 0.082598
We can calculate the sample mean and deviation with the following formulas:
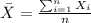
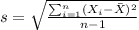
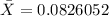 represent the sample mean
represent the sample mean
 population mean
population mean
s=0.000013424 represent the sample standard deviation
n=5 represent the sample size
Part 1
The confidence interval for the mean is given by the following formula:
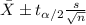 (1)
(1)
The degrees of freedom, given by:

The Confidence level is 0.95 or 95%, and the significance would be
 and
and
 , the critical value would be using the t distribution with 4 degrees of freedom:
, the critical value would be using the t distribution with 4 degrees of freedom:
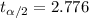
Now we have everything in order to replace into formula (1):
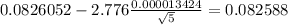

Part 2
The original margin of error is given by:
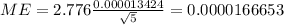
And we want 2/3 of the margin of error so then would be:
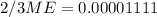
The margin of error is given by this formula:
 (1)
(1)
And on this case we have that ME =0.00001111016 and we are interested in order to find the value of n, if we solve n from equation (1) we got:
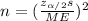 (2)
(2)
Replacing we got:
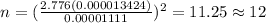
So the answer for this case would be n=12 rounded up to the nearest integer