Question

Suppose n balls are distributed in n boxes in such a way that each ball chooses a box indepen- dently of each other. (a) What is the probability that Box #1 is empty? (b) What is the probability that only Box #1 is empty? (c) What is the probability that only one box is empty? (d) Given that Box #1 is empty, what is the probability that only one box is empty? (e) Given that only one box is empty, what is the probability that Box #1 is empty?

Answer 1

Check the explanation

Explanation:

a) Probability that Box #1 is empty is computed here as:

= Number of ways to distribute each of the the n balls in remaining (n - 1) boxes / Total ways to distribute n balls into n boxes

=
`((n-1)^n)/(n^n) = (1 - (1)/(n))^n`

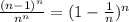
This is the required probability here.

b) Probability that only 1 box is empty is computed here as:

= Number of ways to choose one of the remaining (n - 1) boxes such that it will have 2 balls * Number of ways to select 2 balls of that box* permutation of remaining (n - 2) balls into (n - 2) boxes / Total ways to distribute n balls into n boxes

=
`\frac{\binom{n-1}{1}\binom{n}{2}(n-2)!}{n^n}`

=
`((n-1)n!(n-2)!)/(2n^n)`

=
`(n!(n-1)!)/(2n^n)`

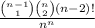
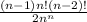
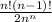
This is the required probability here.

c) Probability that only 1 box is empty is computed here as:

= Number of ways to select a box which would be empty * Probability that only that box would be empty ( from previous part)

=
`(n*n!(n-1)!)/(2n^n)`

=
`((n!)^2)/(2n^n)`

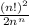
This is the required probability here.

d) Given that box #1 is empty, probability that only 1 box is empty is computed here as:

= Probability that only box 1 is empty / Probability that box 1 is empty

We will use the answers from parts a) and b) here to get:

=
`( (n!(n-1)!)/(2n^n))/(((1 - n)^n)/(n^n))`

=
`(n!(n-1)!)/(2(1-n)^n)`

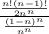
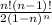
This is the required probability here.

e) Given that only 1 box is empty, probability that box #1 is empty is computed here as:

= 1/n as each box is equally likelt to be empty

Therefore 1/n is the required probability here.