Answer:
a)14.17V
b)32.8 x
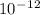 J
J
c)96.9x
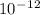 J
J
d) -64x
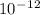 J
J
Step-by-step explanation:
Given:
Area 'A'=7.10cm² =>7.1 x
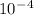 m²
m²
voltage '
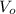 '=4.8 volt
'=4.8 volt
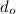 = 2.20mm => 2.2 x
= 2.20mm => 2.2 x
 m
m
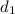 = 6.50mm => 6.5 x
= 6.50mm => 6.5 x
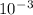 m
m
a) Capacitance
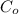 before push is given by:
before push is given by:
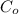 = εA/
= εA/
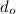 =>
=>
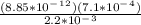
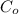 = 2.85 x
= 2.85 x
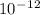 F
F
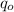 =
=
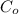
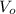 => 2.85 x
=> 2.85 x
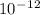 x 4.8
x 4.8
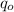 =1.37 x
=1.37 x
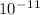 C
C
Capacitance
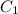 after push is given by:
after push is given by:
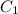 = εA/
= εA/
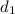 =>
=>
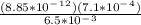
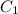 = 9.66 x
= 9.66 x
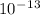 F
F
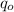 =
=
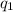
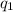 =
=
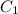
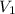
Therefore, the potential difference between the plates
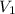 = 1.37 x
= 1.37 x
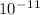 / 9.66 x
/ 9.66 x
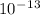 =>14.17V
=>14.17V
b)
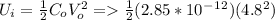
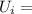 32.8 x
32.8 x
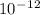 J
J
c)
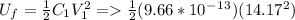
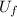 = 96.9x
= 96.9x
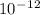 J
J
d) the work required to separate the plates is given by:
workdone=
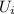 -
-
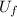 => 32.8 x
=> 32.8 x
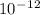 J- 96.9x
J- 96.9x
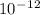 J
J
W≈ -64x
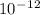 J
J