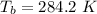Complete Question
The complete question is shown on the first uploaded image
Answer:
The total pressure is
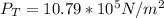
The temperature at the bottom is
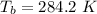
Step-by-step explanation:
From the question we are told that
The length of the glass tube is
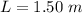
The length of water rise at the bottom of the lake
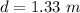
The depth of the lake is
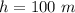
The air temperature is
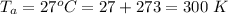
The atmospheric pressure is
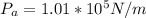
The density of water is
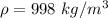
The total pressure at the bottom of the lake is mathematically represented as
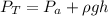
substituting values
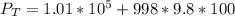
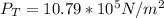
According to ideal gas law
At the surface the glass tube not covered by water at surface
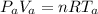
Where is the volume of
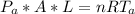
At the bottom of the lake
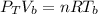
Where
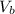 is the volume of the glass tube not covered by water at bottom
is the volume of the glass tube not covered by water at bottom
and
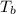 i the temperature at the bottom
i the temperature at the bottom
So the ratio between the temperature at the surface to the temperature at the bottom is mathematically represented as
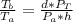
substituting values
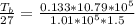
=>