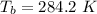Question

A glass tube 1.50 meters long and open at one end is weighted to keep it vertical and is then lowered to the bottom of a lake. When it returns to the surface it is determined that at the bottom of the lake the water rose to within 0.133 meters of the closed end. The lake is 100 meters deep, the air temperature at the surface is 27 "C, atmospheric pressure is 1.01x10s N/m2, and the density of water is 998 kg/m3. a) What is the total pressure at the bottom of the lake

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The total pressure is
`P_T = 10.79*10^(5) N/m^2`

The temperature at the bottom is
`T_b = 284.2 \ K`

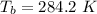
Step-by-step explanation:

From the question we are told that

The length of the glass tube is
`L = 1.50 \ m`

The length of water rise at the bottom of the lake
`d = 1.33 \ m`

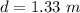
The depth of the lake is
`h = 100 \ m`

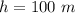
The air temperature is
`T_a = 27 ^oC = 27 +273 = 300 \ K`

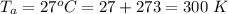
The atmospheric pressure is
`P_a = 1.01 *10^(5) N/m`

The density of water is
`\rho = 998 \ kg/m^3`

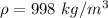
The total pressure at the bottom of the lake is mathematically represented as

`P_T = P_a + \rho g h`

substituting values

`P_T = 1.01*10^(5) + 998 * 9.8 * 100`

`P_T = 10.79*10^(5) N/m^2`

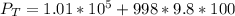
According to ideal gas law

At the surface the glass tube not covered by water at surface

`P_a V_a = nRT_a`

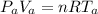
Where is the volume of

`P_a *A * L = nRT_a`

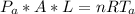
At the bottom of the lake

`P_T V_b = nRT_b`

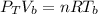
Where
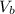`V_b` is the volume of the glass tube not covered by water at bottom

and
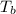`T_b` i the temperature at the bottom

So the ratio between the temperature at the surface to the temperature at the bottom is mathematically represented as

`(T_b)/(T_a) = (d * P_T)/(P_a * h)`

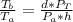
substituting values

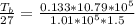
`(T_b)/(27) = (0.133 * 10.79 *10^5)/(1.01 *10^(5) * 1.5)`

=>
`T_b = 284.2 \ K`