Question

The editor of a textbook publishing company is deciding whether to publish a proposed textbook. Information on previous textbooks published show that 20 % are huge​ successes, 30 % are modest​ successes, 30 % break​ even, and 20 % are losers. Before a decision is​ made, the book will be reviewed. In the​ past, 99 % of the huge successes received favorable​ reviews, 70 % of the moderate successes received favorable​ reviews, 40 % of the​ break-even books received favorable​ reviews, and 20 % of the losers received favorable reviews. If the textbook receives a favorable​ review, what is the probability that it will be huge​ success?

Answer 1

34.86% probability that it will be huge​ success

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

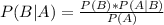
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Receiving a favorable review.

Event B: Being a huge success.

Information on previous textbooks published show that 20 % are huge​ successes

This means that
`P(B) = 0.2`

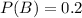
99 % of the huge successes received favorable​ reviews

This means that
`P(A|B) = 0.99`

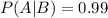
Probability of receiving a favorable review:

20% are huge​ successes. Of those, 99% receive favorable reviews.

30% are modest​ successes. Of those, 70% receive favorable reviews.

30% break​ even. Of those, 40% receive favorable reviews.

20% are losers. Of those, 20% receive favorable reviews.

Then

`P(A) = 0.2*0.99 + 0.3*0.7 + 0.3*0.4 + 0.2*0.2 = 0.568`

Finally

`P(B|A) = (P(B)*P(A|B))/(P(A)) = (0.2*0.99)/(0.568) = 0.3486`

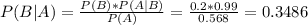
34.86% probability that it will be huge​ success