Question

Qualification exams for becoming a state-certified welding inspector are based on multiple-choice tests. As in any multiple-choice test, there is a possibility that someone who is simply guessing the answers to each question might pass the test. Let x denote the number of correct answers given by a person who is guessing each answer on a 25-question exam, with each question having five possible answers (for each question, assume only one of the five choices is correct).(a) What type of probability distribution does x have?(b) For the 25-question test, what are the mean and standard deviation of x?(c) The exam administrators want to make sure that there is a very small chance, say, 1%, that a person who is guessing will pass the test. What minimum passing score should they allow on the exam to meet this requirement?

Answer 1

(a) The probability distribution of the random variable X is Binomial.

(b) The mean and standard deviation of the 25-question test are 5 and 2 respectively.

(c) The value of x is 0.34.

Explanation:

The random variable X is defined as the number of correct answers given by a person who is guessing each answer on a 25-question exam.

There are five possible answer for every question.

This implies that the probability of getting a correct answer is:

P (X) = 0.20.

There are a total of n = 25 questions.

Every answer is independent of the others.

(a)

The random variable X has finite number of independent trials (i.e. 25 questions). There are only two outcomes for each trial, i.e. Success = correct answer and Failure = wrong answer. Each trial has the same probability of success (, i.e. P (X) = 0.25).

Thus, the probability distribution of the random variable X is Binomial with parameters n = 25 and p = 0.20.

(b)

Compute the mean of the random variable X as follows:

`E(X)=np\\=25* 0.20\\=5`

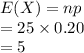
Compute the standard deviation of the random variable X as follows:

`SD(X)=√(np(1-p))\\=√(25* 0.20* (1-0.20))\\=2`

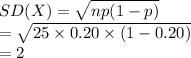
Thus, the mean and standard deviation of the 25-question test are 5 and 2 respectively.

(c)

The sample is large and the probability of success is close to 0.50.

So a Normal approximation to binomial can be applied to approximate the distribution of X if the following conditions are satisfied:

1. np ≥ 5

2. n(1 - p) ≥ 5

Check the conditions as follows:

`np=25* 0.20=5=5\\\\n(1-p)=25* (1-0.20)=20>5`

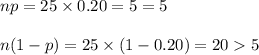
Thus, a Normal approximation to binomial can be applied.

So,
`X\sim N(5, 2^(2))`

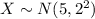
It is provided that the minimum passing score foe the test is such that only 1% of students who are guessing will pass the test.

That is P (X < x) = 0.01.

⇒ P (Z < z) = 0.01

The value of z is -2.33.

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\\\-2.33=(x-5)/(2)\\\\x=5-(2.33* 2)\\\\x=0.34`

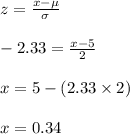
Thus, the value of x is 0.34.