Question

You must determine the length of a long, thin wire that is suspended from the ceiling in the atrium of a tall building. A 2.00-cm-long piece of the wire is left over from its installation. Using an analytical balance, you determine that the mass of the spare piece is 14.5 μg . You then hang a 0.400-kg mass from the lower end of the long, suspended wire. When a small-amplitude transverse wave pulse is sent up that wire, sensors at both ends measure that it takes the wave pulse 24.7 ms to travel the length of the wire.

Answer 1

Step-by-step explanation:

Let L be the length of the wire.

velocity of pulse wave v = L / 24.7 x 10⁻³ = 40.48 L m /s

mass per unit length of the wire m = 14.5 x 10⁻⁶ x 10⁻³ / 2 x 10⁻² kg / m

m = 7.25 x 10⁻⁷ kg / m

Tension in the wire = Mg , M is mass hanged from lower end.

= .4 x 9.8

= 3.92 N

expression for velocity of wave in the wire

`v = \sqrt{(T)/(m) }` , T is tension in the wire , m is mass per unit length of wire .

40.48 L =
`\sqrt{(3.92)/(7.25*10^(-7)) }`

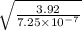
1638.63 L² = 3.92 / (7.25 x 10⁻⁷)

L² = 3.92 x 10⁷ / (7.25 x 1638.63 )

L² = 3299.64

L = 57.44 m /s