Answer:
The probability that he drove the small car is 0.318.
Explanation:
We are given that a friend who works in a big city owns two cars, one small and one large. One-quarter of the time he drives the small car to work, and three-quarters of the time he takes the large car.
If he takes the small car, he usually has little trouble parking and so is at work on time with probability 0.7. If he takes the large car, he is on time to work with probability 0.5.
Let the Probability that he drives the small car = P(S) =
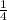 = 0.25
= 0.25
Probability that he drives the large car = P(L) =
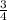 = 0.75
= 0.75
Also, let WT = event that he is at work on time
So, Probability that he is at work on time given that he takes the small car = P(WT / S) = 0.7
Probability that he is at work on time given that he takes the large car = P(WT / L) = 0.5
Now, given that he was at work on time on a particular morning, the probability that he drove the small car is given by = P(S / WT)
We will use the concept of Bayes' Theorem for calculating above probability;
So, P(S / WT) =
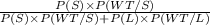
=
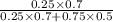
=
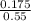
= 0.318
Hence, the required probability is 0.318.