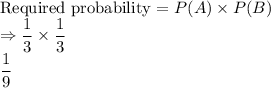Question

Drawing a 1, 2, or 3 from 9 cards numbered 1-9, replacing the card,

and drawing a 7, 8, or 9
1/3
3/8
C
1/9
d
1/12​

Answer 1

The required probability is option
`C)\ (1)/(9)`

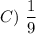
Explanation:

There are a total of 9 cards.

Total number of cases = 9

Let A be the event of choosing 1, 2 or 3.

Total number of favorable cases for event A = 3

Let B be the event of choosing 7, 8 or 9.

Total number of favorable cases for event B = 3

Formula for finding probability of an event E is:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

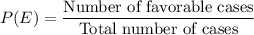
Finding P(A), using the formula:

`P(A) = (3)/(9)\\\Rightarrow (1)/(3)`

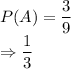
Now, it is given that the card is replaced, so again total number of cases are 9.

For finding P(B), using the formula:

`P(B) = (3)/(9)\\\Rightarrow (1)/(3)`

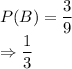
To find the probability that events A and B both happen, we can simply multiply P(A) and P(B) because these are independent events.

`\text{Required probability = }P(A) * P(B)\\\Rightarrow (1)/(3) * (1)/(3) \\(1)/(9)`