Question

A prism has an isosceles triangle bases with leg lengths of 5 inches 5 in and 8 inches and a height of 3 in the distance between the bases is 12 in find the surface area show your work

Answer 1

240 in²

Explanation:

The prism has an isosceles triangle with the following data:

- Two lengths = 5 inches

- Other length = 8 inches

- Height = 12 inches

Since the prism consist of 2 triangle bases and three rectangular faces, the surface area (SA) of the prism can be calculated as follows:

`SA = SA_(b1) + SA_(b2) + SA_(f1) + SA_(f2) + SA_(f3)`

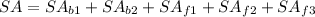
Where:

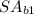`SA_(b1)` and
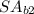`SA_(b2)` are the surface areas of the two triangle bases.

`SA_(f1)`,
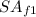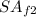`SA_(f2)` and
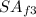`SA_(f3)`: are the surface areas of the three rectangular faces.

The surface area of the triangle bases can be calculated as follows:

`SA_(b1) = SA_(b2) = (b*h)/(2)`

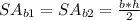
Where:

b: is the base = lenght of 8 inches

h: is the height = 3 inches

`SA_(b1) = SA_(b2) = (8*3)/(2) = 12 in^(2)`

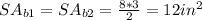
Now, we need to find the surface area of the rectangular faces using the following data:

Rectangular face 1 = rectangular face 2:

- One side = 12 inches

- Other side = 5 inches

Rectangular face 3:

- One side = 12 inches

- Other side = 8 inches

Hence, the SA of the rectangular face 1 and rectangular face 2 is:

`SA_(f1) = SA_(f2) = 12*5 = 60 in^(2)`

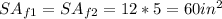
And the SA of the rectangular face 3 is:

`SA_(f3) = 12*8 = 96 in^(2)`

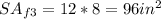
Finally, the SA of the prism is:

`SA = SA_(b1) + SA_(b2) + SA_(f1) + SA_(f2) + SA_(f3)`

`SA = 2*12 + 2*60 + 96 = 240 in^(2)`

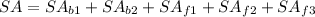
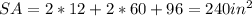
Therefore, the surface area of the prism is 240 in².

I hope it helps you!

Answer 2

240 Square Inches

Explanation:

See the attached diagram

The Isosceles Triangle based prism consists of two triangles of equal area, to rectangles of equal area and the rectangle at the base.

Therefore:

Surface Area of the Prism =Surface Area of Two Triangular Base+Area of three Rectangles

Area of one Triangular Base=0.5 X 8 x 3 =12 Square inches

Area of Rectangle 1=5 x 12 =60 Square Inch

Area of Rectangle 2=5 x 12 =60 Square Inch

Area of Rectangle 3=8 x 12 =96 Square Inch

Therefore:

Surface Area of the Prism=2(12)+2(60)+96

=240 Square Inches