Answer:
0.545 = 54.5% probability that it came from machine A
Explanation:
Bayes Theorem:
Two events, A and B.
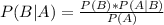
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.
In this question:
Event A: Defective.
Event B: Coming from machine A.
Machine A is responsible for 30%
This means that
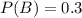
10% of the output from machine A is defective
This means that
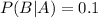
Probability of being defective:
Machine A is responsible for 30%. Of those, 10% are defective.
Machine B is responsible for 20%. Of those, 5% are defective.
Machine C is responsible for 100 - (30+20) = 50%. Of those, 3% are defective. Then
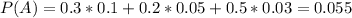
Finally:
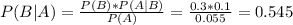
0.545 = 54.5% probability that it came from machine A