Answer:
c) Two sample t-test
Step-by-step explanation:
Given data
Golfer 1 2 3 4
Brand1 (x) 93 88 112 79
Brand 2 (y) 95 86 111 77
Mean of x =
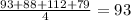
x⁻ = 93
Mean of y
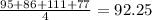
y ⁻ = 92.25
Given data
Brand1 (x) : 93 88 112 79
Brand 2 (y) : 95 86 111 77
x- x⁻ : 0 -5 19 -14
y -y ⁻ : 2.75 -6.25 18.75 -15.25
(x- x⁻)² : 0 25 361 196
( y -y ⁻ )² : 7.5625 39.0625 351.5625 232.5625
S² =
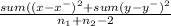
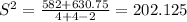
S = 14.21706
Null hypothesis: H₀: There is no significant difference between the means
Alternative hypothesis: H₁: There is significant difference between the means
Student's t test for difference for means
The test statistic


on calculation , we get
t = 0.0746
Degrees of freedom ν = n₁ +n₂ -2 = 4+4-2 =6
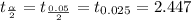
The calculated value t = 0.0746 < 2.447 at 0.05 level of significance
null hypothesis is accepted
Conclusion:-
There is no significant difference between the means