Question

Four golfers are asked to play a round of golf each on two consecutive Saturday afternoons. During the first round, one of two club types is to be used. During the second round, another club type is to be used. The order in which a golfer uses each brand is determined randomly. Scores are recorded. The results are given below.

Golfer Brand 1 Brand 2
1 93 95
2 88 86
3 112 111
4 79 77

To determine if the mean scores differ by brand of club, we would use

a. the one-sample t test.
b. matched pairs t test.
c. two-sample t test.
d. Any of the above are valid. It is at the experimenter's discretion.

Answer 1

The matched pairs t-test is the correct method for analyzing the difference in golfers' scores with two different brands of clubs, as each golfer serves as their control.

Step-by-step explanation:

The appropriate test to determine if the mean scores differ by brand of club is b. matched pairs t-test. Since the data consists of scores from the same golfers using two different brands of clubs in a controlled setting (meaning, the same golfer's scores are paired with each type of golf club), the analysis compares two related samples. In matched pairs designs, we test the differences by subtracting one measurement from the other. The golfers serve as their controls, eliminating variations between different individuals' performances, which could affect the scores. This is a classic scenario of a paired sample t-test, where each golfer's scores with Brand 1 are paired with their scores with Brand 2, and the difference in scores is analyzed.

Answer 2

c) Two sample t-test

Step-by-step explanation:

Given data

Golfer 1 2 3 4

Brand1 (x) 93 88 112 79

Brand 2 (y) 95 86 111 77

Mean of x =

`(93+88+112+79)/(4) = 93`

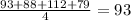
x⁻ = 93

Mean of y

`(95+86+111+77)/(4) = 92.25`

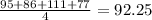
y ⁻ = 92.25

Given data

Brand1 (x) : 93 88 112 79

Brand 2 (y) : 95 86 111 77

x- x⁻ : 0 -5 19 -14

y -y ⁻ : 2.75 -6.25 18.75 -15.25

(x- x⁻)² : 0 25 361 196

( y -y ⁻ )² : 7.5625 39.0625 351.5625 232.5625

S² =
`(sum((x- x^(-) )^(2) +sum (y- y^(-) )^(2) )/(n_(1)+n_(2) -2 )`

`S^(2) = (582+630.75)/(4+4-2) = 202.125`

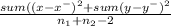
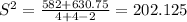
S = 14.21706

Null hypothesis: H₀: There is no significant difference between the means

Alternative hypothesis: H₁: There is significant difference between the means

Student's t test for difference for means

The test statistic

`t = \frac{x^(-) -y^(-) }{\sqrt{S^(2)((1)/(n_(1) ) +(1)/(n_(2) ) } }`

`t = \frac{93 -92.25}{\sqrt{202.125((1)/(4 ) +(1)/(4 ) } }`

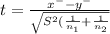
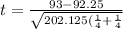
on calculation , we get

t = 0.0746

Degrees of freedom ν = n₁ +n₂ -2 = 4+4-2 =6

`t_{(\alpha )/(2) } = t_{(0.05)/(2) } = t_(0.025) = 2.447`

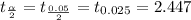
The calculated value t = 0.0746 < 2.447 at 0.05 level of significance

null hypothesis is accepted

Conclusion:-

There is no significant difference between the means