Question

A marketing survey involves brand recognition in New York and California. Of 147 New Yorkers surveyed, 79 were familiar with the brand while 78 out of 147 Californians knew this brand as well. Assume that you plan to test the claim that the proportion of New Yorkers who recognize this brand differs from the proportion of Californians who do the same, i.e., p1 ≠ p2. Use the given information to find the pooled sample proportion begin mathsize 14px style p with bar on top end style. Round your answer to three decimal places.

Answer 1

`z=\frac{0.537-0.531}{\sqrt{0.534(1-0.534)((1)/(147)+(1)/(147))}}=0.103`

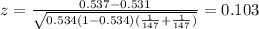
Now we can calculate the p value with the following probability taking in count the alternative hypothesis:

`p_v =2*P(Z>0.103) =0.918`

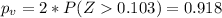
For this case since the p value is large enough we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that we have significant differences between the two proportions analyzed.

Explanation:

Information provided

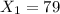`X_(1)=79` represent the number of New Yorkers familiar with the brand

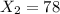`X_(2)=78` represent the number of Californians familiar with the brand

`n_(1)=147` sample of New Yorkers

`n_(2)=147` sample of Californians

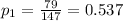`p_(1)=(79)/(147)=0.537` represent the proportion New Yorkers familiar with the brand

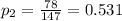`p_(2)=(78)/(147)=0.531` represent the proportion of Californians familiar with the brand

`\hat p` represent the pooled estimate of p

z would represent the statistic

`p_v` represent the value

System of hypothesis

We want to verify if the two proportions of interest for this case are equal, the system of hypothesis would be:

Null hypothesis:
`p_(1) = p_(2)`

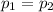
Alternative hypothesis:
`p_(1) \\eq p_(2)`

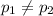
The statistic would be given by:

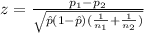`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(79+78)/(147+147)=0.534`

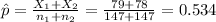
Repalcing the info given we got:

`z=\frac{0.537-0.531}{\sqrt{0.534(1-0.534)((1)/(147)+(1)/(147))}}=0.103`

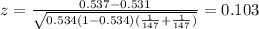
Now we can calculate the p value with the following probability taking in count the alternative hypothesis:

`p_v =2*P(Z>0.103) =0.918`

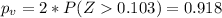
For this case since the p value is large enough we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that we have significant differences between the two proportions analyzed.