Answer:
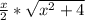 +
+
 *LN(|
*LN(|
 |) +C
|) +C
Explanation:
we will have to do a trig sub for this
use x=a*tanθ for sqrt(x^2 +a^2) where a=2
x=2tanθ, dx= 2 sec^2 (θ) dθ
this turns
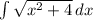 into integral(sqrt( [2tanθ]^2 +4) * 2sec^2 (θ) )dθ
into integral(sqrt( [2tanθ]^2 +4) * 2sec^2 (θ) )dθ
the sqrt( [2tanθ]^2 +4) will condense into 2sec^2 (θ) after converting tan^2(θ) into sec^2(θ) -1
then it simplifies into integral(4*sec^3 (θ)) dθ
you will need to do integration by parts to work out the integral of sec^3(θ) but it will turn into (1/2)sec(θ)tan(θ) + (1/2) LN(|sec(θ)+tan(θ)|) +C
then you will need to rework your functions of θ back into functions of x
tanθ will resolve back into
 (see substitutions) while secθ will resolve into
(see substitutions) while secθ will resolve into

sec(θ)=
 is from its ratio identity of hyp/adj where the hyp. is
is from its ratio identity of hyp/adj where the hyp. is
 and adj is 2 (see tan(θ) ratio)
and adj is 2 (see tan(θ) ratio)
after resolving back into functions of x, substitute ratios for trig functions:
=
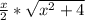 +
+
 *LN(|
*LN(|
 |) +C
|) +C