Question

A 50-cm x 50-cm circuit board that contains 121 square chips on one side is to be cooled by combined natural convection and radiation by mounting it on a vertical surface in a room at 25 °C. Each chip dissipates 0.18 W of power, and the emissivity of the chip surfaces is 0.7. Assuming the heat transfer from the back side of the circuit board to be negligible, and the temperature of the surrounding surfaces to be the same as the air temperature of the room, determine the surface temperature of the chips. Evaluate air properties at a film temperature of 30 °C and 1 atm pressure. Is this a good assumption?

Answer 1

Ts = 311.86 K = 38.86°C

Step-by-step explanation:

The convection heat transfer coefficient for vertical orientation of the board is given by the formula:

`h = 1.42((T_(s) - T_(f) )/(L))^(0.25)`

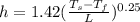
where,

h = heat transfer coefficient

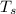`T_(s)` = surface temperature

`T_(f)` = Temperature of fluid (air) = 30°C + 273 = 303 K

L = Characteristic Length = 50 cm = 0.5 m

Since the heat transfer through convection is given as:

`Q_(conv) = hA_(s)(T_(s) - T_(f))`

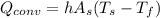
using value of h, we get:

`Q_(conv) = 1.42((T_(s) - T_(f) )/(L))^(0.25) A_(s) (T_(s) - T_(f) )`

`Q_(conv) = 1.42 A_(s) ((T_(s) - T_(f) )^(1.25) )/(L^(0.25) )`

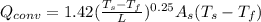
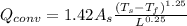
where,

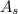`A_(s)` = Surface Area = (0.5 m)(0.5 m) = 0.25 m²

Now, the radiation heat transfer is given by:

`Q_(rad) =` εσ
`A_(s) [(T_(s))^(4) - (T_(surr))^(4)]`

where,

ε = emissivity of surface = 0.7

σ = Stefan Boltzman Constant = 5.67 x 10⁻⁸ W/m².k⁴

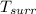`T_(surr)` = Temperature of surroundings = 25°C +273 = 298 k

Now, the total heat transfer rate will be:

`Q_(total) = Q_(conv) + Q_(rad)`

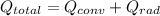
using values:

`Q_(total) =`
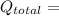
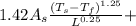`1.42 A_(s) ((T_(s) - T_(f) )^(1.25) )/(L^(0.25) ) +` εσ
`A_(s) [(T_(s))^(4) - (T_(surr))^(4)]`

we know that the total heat transfer from the board can be found out by:

`Q_(total) = (0.18 W) (121) = 21.78 W`

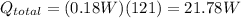
using values in the equation:

21.78 = (1.42)(0.25)
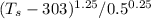`(T_(s) - 303)^(1.25)/0.5^(0.25)` + (0.7)(5.67 x 10⁻⁸)(0.25)
`[(T_(s))^(4) - 298^(4)]`

21.78 = (0.4222)
`(T_(s) - 303)^(1.25)` + 9.922 x 10⁻⁹
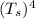`(T_(s) )^(4)` - 78.25

100.03 = (0.4222)
`(T_(s) - 303)^(1.25)`+ 9.922 x 10⁻⁹
`(T_(s) )^(4)`

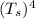
Solving this equation numerically by Newton - Raphson Method (Here, any numerical method or an equation solver can be used), we get the value of Ts to be:

Ts = 311.86 K = 38.86°C

The film temperature is the average of surface temperature and surrounding temperature. Therefore,

Film Temperature = (25°C + 38.86°C)/2 = 31.93°C

Since, this is very close to 30°C.

Hence, the assumption is good.