1 Answer

Arasu · Answer 1 · 2021-02-20T03:40:04+0000

We have been given that a right triangle with integer sides has area equal to 30. We are asked to find the length of hypotenuse of right triangle.

We know that area of triangle is half the product of its base length and height.

Since our given triangle is a right triangle, so its base and height will be legs of right triangle.

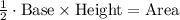
$(1)/(2)\cdot\text{Base}* \text{Height}=\text{Area}$

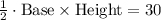
$(1)/(2)\cdot\text{Base}* \text{Height}=30$

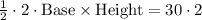
$(1)/(2)\cdot 2\cdot\text{Base}* \text{Height}=30\cdot 2$

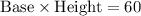
$\text{Base}* \text{Height}=60$

This means that product of two bases is 60.

Now we need to find two multiples of 60 such that they are make a right triangle.

Multiples of 60:

1, 60

2, 30

3, 20

4, 15

5, 12

6, 10

We know that (5, 12 and 13) is a Pythagoras triplet.

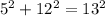
5^2+12^2=13^2

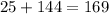
25+144=169

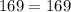
169=169

Therefore, the hypotenuse of right triangle is 13 units.

Please log in or register to add a comment.