Answer:
We conclude that the percentage of employed workers who have registered to vote exceeds the percentage of unemployed workers who have registered to vote.
Explanation:
We are given that 513 employed persons and 604 unemployed persons are independently and randomly selected, and that 287 of the employed persons and 280 of the unemployed persons have registered to vote.
Let
 = percentage of employed workers who have registered to vote.
= percentage of employed workers who have registered to vote.
 = percentage of unemployed workers who have registered to vote.
= percentage of unemployed workers who have registered to vote.
So, Null Hypothesis,
 :
:
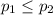 {means that the percentage of employed workers who have registered to vote does not exceeds the percentage of unemployed workers who have registered to vote}
{means that the percentage of employed workers who have registered to vote does not exceeds the percentage of unemployed workers who have registered to vote}
Alternate Hypothesis,
 :
:
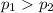 {means that the percentage of employed workers who have registered to vote exceeds the percentage of unemployed workers who have registered to vote}
{means that the percentage of employed workers who have registered to vote exceeds the percentage of unemployed workers who have registered to vote}
The test statistics that would be used here Two-sample z test for proportions;
T.S. =
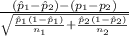 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of employed workers who have registered to vote =
= sample proportion of employed workers who have registered to vote =
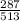 = 0.56
= 0.56
 = sample proportion of unemployed workers who have registered to vote =
= sample proportion of unemployed workers who have registered to vote =
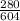 = 0.46
= 0.46
 = sample of employed persons = 513
= sample of employed persons = 513
 = sample of unemployed persons = 604
= sample of unemployed persons = 604
So, the test statistics =

= 3.349
The value of z test statistics is 3.349.
Now, at 0.05 significance level the z table gives critical value of 1.645 for right-tailed test.
Since our test statistic is more than the critical value of z as 3.349 > 1.645, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.
Therefore, we conclude that the percentage of employed workers who have registered to vote exceeds the percentage of unemployed workers who have registered to vote.