Question

What is the probability that a data value in a normal distribution is between a z-score of -0.28 and a z-score of 0.64? Round your answer to the nearest tenth of a percent. A. 90.9% B. 58.1% C. 34.9% D. 73.3%

Answer 1

`P(-0.28 <Z< 0.64) = P(Z<0.64) -P(Z<-0.28)`

`P(Z<0.64) =0.739`

`P(Z<-0.28) =0.390`

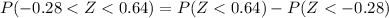
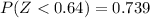
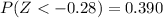
And with the difference we got: 0.739-0.390 = 0.349

And if we convert the probability to % we got 0.349*100 = 34.9%. And the best answer would be:

C. 34.9%

Explanation:

For this case we want this probability:

`P(-0.28 <Z< 0.64)`

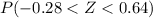
And we can find this probability using the normal standard distribution and with the following difference:

`P(-0.28 <Z< 0.64) = P(Z<0.64) -P(Z<-0.28)`

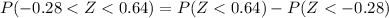
If we find the individual probabilities we got:

`P(Z<0.64) =0.739`

`P(Z<-0.28) =0.390`

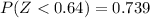
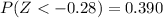
And with the difference we got: 0.739-0.390 = 0.349

And if we convert the probability to % we got 0.349*100 = 34.9%. And the best answer would be:

C. 34.9%