For
 between
between
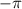 and
and
 , we have
, we have
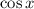 is continuous over its domain, so the intermediate value theorem tells us that
is continuous over its domain, so the intermediate value theorem tells us that
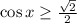
is true for
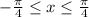 .
.
For all
 , we take into account that
, we take into account that
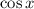 is
is
 -periodic, so the above inequality can be expanded to
-periodic, so the above inequality can be expanded to
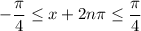
where
 is any integer. Equivalently,
is any integer. Equivalently,
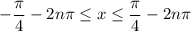
To get the corresponding solution set for
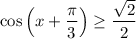
simply replace
 with
with
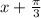 :
:

