Question

What is the slope of a line that passing through the points ( 6 , -10 ) and ( 8, -18) ?

Answer 1

Slope = -4

Explanation:

Given:

• Point 1: (6,-10)

• Point 2: (8,-18)

Rate of change (Slope) formula:

`\text{Slope} = \frac{\text{Rise}}{\text{Run}} = \frac{\text{y}_(2) - \text{y}_(1)}{\text{x}_(2) - \text{x}_(1) }`

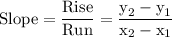
Where:

• y₂ = y-coordinate of second point = -18

• y₁ = y-coordinate of first point = -10

• x₂ = x-coordinate of second point = 8

• x₁ = x-coordinate of first point = 6

Substitute the coordinates of the given points in the formula to determine the slope of the line (Rate of change).

`\implies \text{Slope} = ((-18) - (-10))/(8 - 6 )`

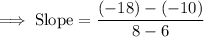
Finally, let's simplify the fraction on the right hand side as needed.

`\implies\text{Slope} = ((-18) + 10)/(8 - 6 )`

`\implies \text{Slope} = (-8)/(2 ) = -4`

Therefore, the slope of a line that passes through (6 , -10 ) and (8, -18) is -4.