Answer:
Step-by-step explanation:
y = y₀ cos
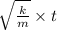
a )
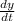 = - y₀ x
= - y₀ x
 sin (
sin (
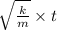 )
)
b ) If m = 4m
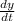 = - y
= - y
 sin (
sin (
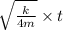 )
)
Magnitude of velocity will be decreased .
c )
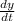 = - y
= - y
 sin (
sin (
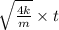 )
)
magnitude of velocity will be increased .
d )
velocity = - y₀
 sin(
sin(
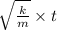 )
)
= L
 X 0
X 0
= L s⁻¹
= m /s
unit of velocity is consistent .