Answer:
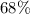
Explanation:
Let A be the event that Daniel receives call from SeaWorld.
Probability of event A, P(A) =

Let B be the event that Daniel receives call from Central Park Zoo.
Probability of event B, P(B) =

Probability that Daniel receives calls from both SeaWorld and Central Park Zoo:
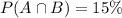
We know that formula:
Probability that Daniel receives call from either SeaWorld or Central Park Zoo but not both:
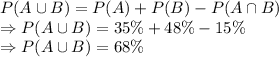
Hence, required probability is
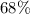 .
.