Question

A set of sofa prices are normally distributed with a mean of 2500 dollars and a standard deviation of 200 dollars.

A leather sofa has a price of 2410 dollars.
What proportion of sofa prices are higher than the price of the leather sofa?
You may round your answer to four decimal places.

Answer 1

0.6736

Explanation:

khan academy

Answer 2

We have been given that a of sofa prices are normally distributed with a mean of 2500 dollars and a standard deviation of 200 dollars. A leather sofa has a price of 2410 dollars. We are asked to find the proportion of sofa prices that are higher than the price of the leather sofa.

First of all, we will find the z-score corresponding to sample score 2410.

`z=(x-\mu)/(\sigma)`

`z=(2410-2500)/(200)`

`z=(-90)/(200)`

`z=-0.45`

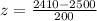
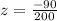
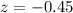
Now we need to find area under normal curve that is greater than z-score of
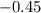`-0.45` that is
`P(z>-0.45)`.

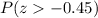Using formula
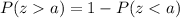`P(z>a)=1-P(z<a)`, we will get:

`P(z>-0.45)=1-P(z<-0.45)`

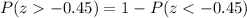
Now we will find area under curve using normal distribution table.

`P(z>-0.45)=1-0.32636`

`P(z>-0.45)=0.67364`

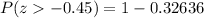
Upon rounding to 4 decimal places, we will get:

`P(z>-0.45)\approx 0.6736`

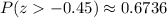
Therefore, approximately 0.6736 of sofa prices are higher than the price of the leather sofa.