Question

One gram of Uranium averages release 1.01 KJ (10^7) of energy. How much mass could be converted to energy to release this much energy?

Answer 1

The amount of mass that needs to be converted to release that amount of energy is
`1.122 X 10^(-7) kg`

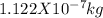
Step-by-step explanation:

From Albert Einstein's Energy equation, we can understand that mass can get converted to energy, using the formula

`E= \Delta mc^(2)`

where
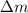`\Delta m` = change in mass

c = speed of light =
`3 * 10 ^(8)m/s`

Making m the subject of the formula, we can find the change in mass to be

`\Delta m = (E)/(c^(2))= (1.01 * 10^(3) * 10^(7))/((3 * 10^(8))^(2))= 1.122 * 10 ^(-7)kg`

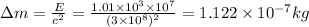
There fore, the amount of mass that needs to be converted to release that amount of energy is 1.122 X 10 ^-7 kg