Answer:

And we can find the nnumber of deviations from the mean for each limit given:
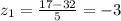
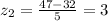
So we are 3 deviation from the mean and using the empirical rule we know that within 3 deviations from the mean we have 99.7% of the values
Explanation:
Let X the random variable that represent the amount of time it takes him to arrive, and for this case we know the distribution for X is given by:
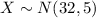
Where
 and
and
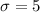
We want to find this probability:
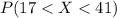
And we can use the z score formula given by:

And we can find the nnumber of deviations from the mean for each limit given:
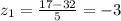
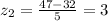
So we are 3 deviation from the mean and using the empirical rule we know that within 3 deviations from the mean we have 99.7% of the values