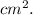Question

The paper cup is 9 cm tall and the circular opening has a radius of 2.5 cm.

What is the minimum amount of paper needed to make the paper cup to the nearest whole cm² assuming no overlap in the paper?

Answer 1

The minimum amount of paper needed to make the paper cup to the nearest whole cm² is approximately 283 cm².

Step-by-step explanation:

To find the minimum amount of paper needed to make the paper cup, we need to calculate the surface area of the cup. The formula for the surface area of a cylinder is:

A = 2πrh + π
`r^2`

Given that the height (h) of the cup is 9 cm and the radius (r) of the circular opening is 2.5 cm, we can plug in the values to calculate the surface area:

A = 2 × 3.14159 × 2.5 × 9 + 3.14159 ×
`2.5^2`

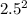
Simplifying the equation, we get:

A ≈ 282.74
`cm^2`

Rounding to the nearest whole , the minimum amount of paper needed is approximately 283
`cm^2.`